QPU Solvers: Minor-Embedding#
The D‑Wave QPU minimizes the energy of an Ising spin configuration whose pairwise interactions lie on the edges of a QPU working graph, such as the Pegasus graph of an Advantage system. To solve an Ising spin problem with arbitrary pairwise interaction structure, the corresponding graph must be minor embedded into a QPU’s graph.
There are algorithms that can embed a problem of \(N\) variables in at most \(N^2\) qubits.
Ocean software’s minorminer provides embedding tools.
This chapter presents the following embedding topics:
Global Versus Local#
Global embedding models each constraint as a BQM, adds all constraint models, and maps the aggregate onto the QPU graph. Advantages of this method are that it typically requires fewer qubits and shorter chains.
Locally structured embedding models each constraint locally within a subgraph, places the local subgraphs within the QPU graph, and then connects variables belonging to multiple local subgraphs. Advantages of this method, when the scopes of constraints are small, are typically that it is more scalable to large problems, requires less precision for parameters, and enforces qubit chains with lower coupling strengths.
Example#
The two graphics below compare local and global embeddings onto an Advantage QPU of a BQM represented by a graph composed of three \(K_5\) cliques (fully connected five-node graphs), sparsely interconnected.
Figure 56 shows a local embedding: each \(K_5\) subgraph is manually embedded using the
FixedEmbeddingCompositeclass into a \(K_{4,4}\)-like structure of the Pegasus graph.Figure 57 shows a global embedding: the entire BQM is embedded using the
EmbeddingCompositeclass.
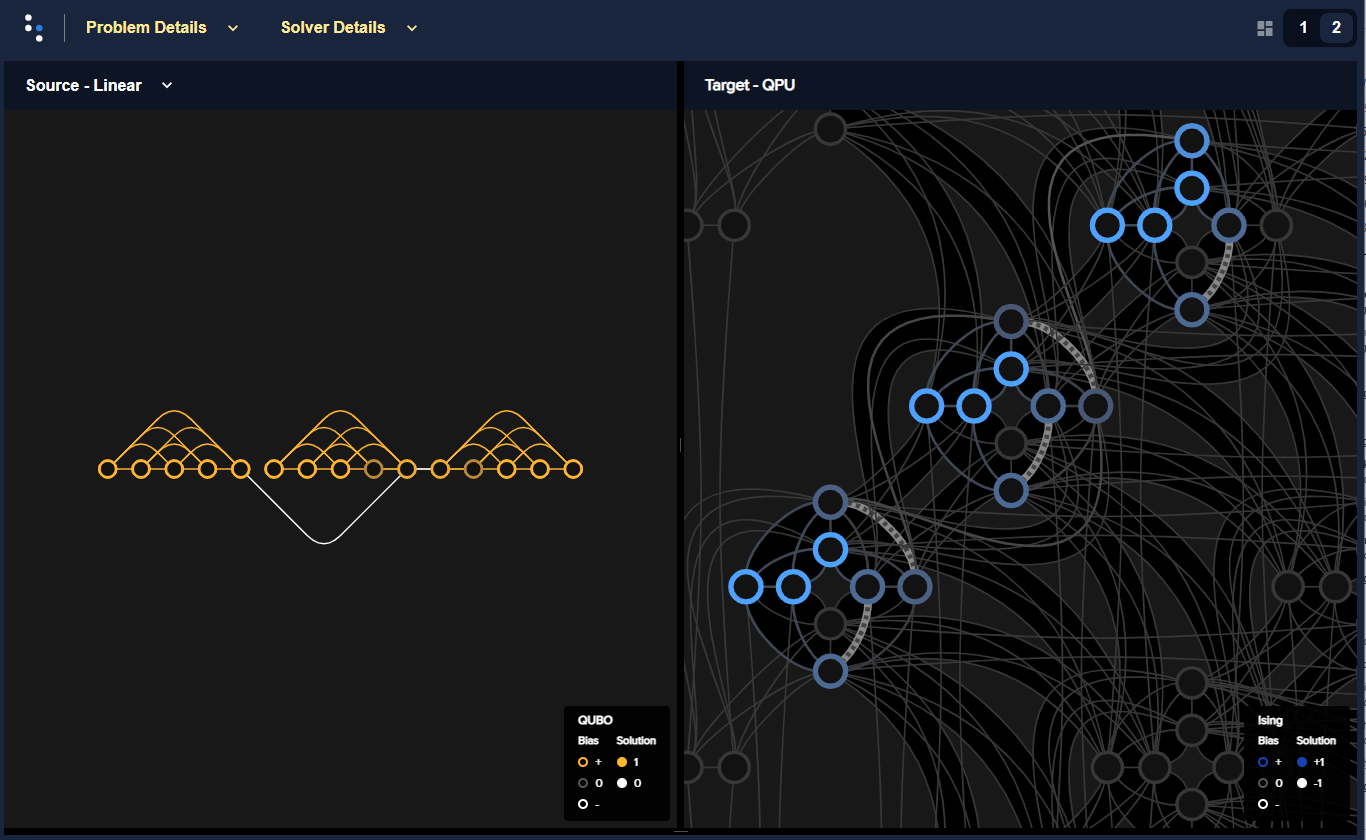
Fig. 56 Example of local embedding for a BQM represented by a graph of three connected \(K_5\) cliques.#
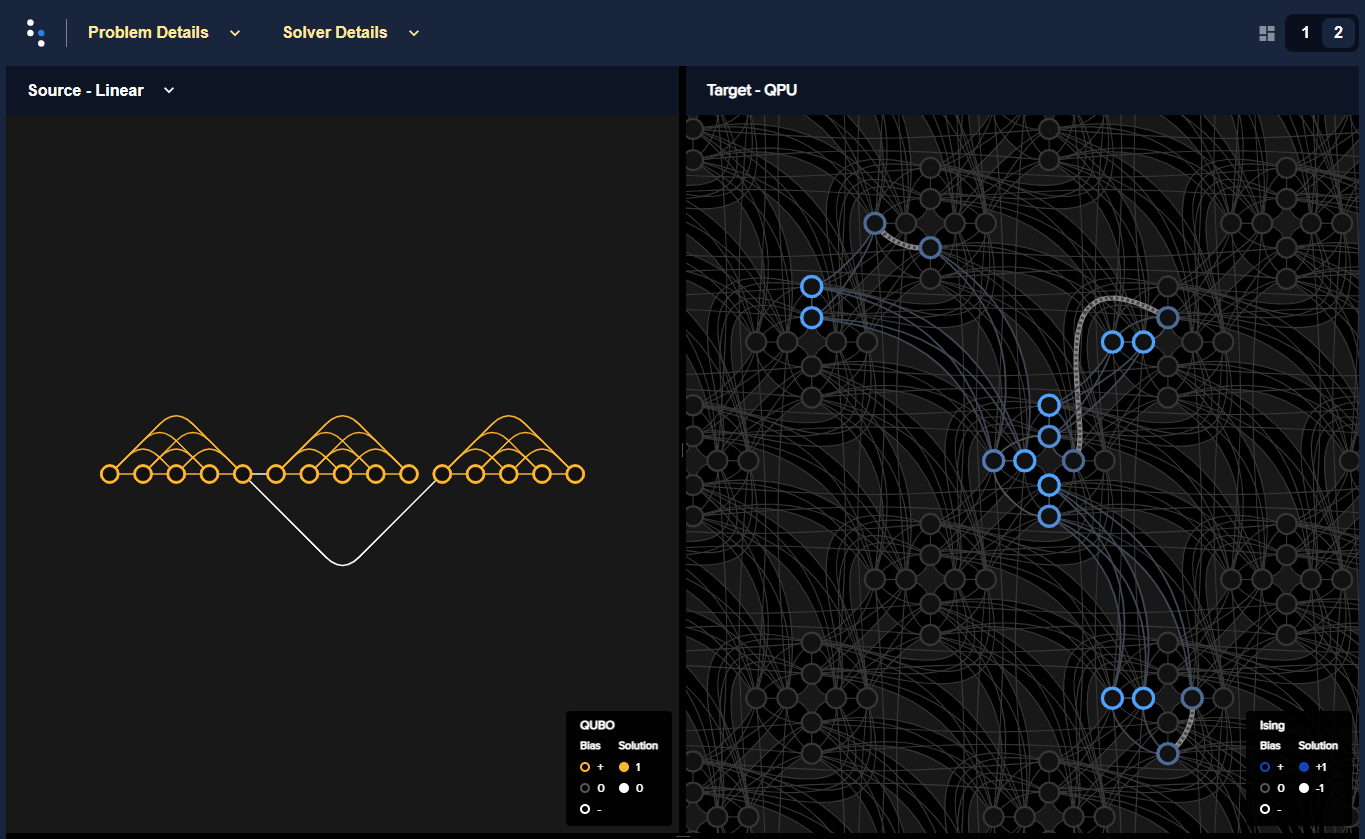
Fig. 57 Example of global embedding for a BQM represented by a graph of three connected \(K_5\) cliques.#
In this small example, global embedding is likely more performant but for a larger number of repeated subgraphs, local emebedding with its repeated structure likely would keep chains shorter and uniform across the entire problem (assuming simple and sparse connectivity between parts).
Further Information#
[Bia2016] compares global and local methods of embedding in the context of CSPs and discusses a rip-up and replace method.
[Boo2016] discusses clique minor generation.
[Cai2014] gives a practical heuristic for finding graph minors.
[Jue2016] discusses using FPGA-like routing to embed.
[Ret2017] describes embedding quantum-dot cellular automata networks.
Chain Management#
Similar to Lagrangian relaxation, you map a given problem’s variable \(s_i\) onto chain \(\{q_i^{(1)}, \cdots, q_i^{(k)}\}\) while encoding equality constraint \(q_i^{(j)} = q_i^{(j')}\) as an Ising penalty \(-M q_i^{(j)} q_i^{(j')}\) of weight \(M > 0\).
The following considerations and recommendations apply to chains.
Prefer short chains to long chains.
Prefer uniform chain lengths to uneven chains.
Balance chain strength and problem range. Estimate chain strength and set just slightly above the minimum threshold needed, using strategies for auto-adjusting these chains. When mapping a problem’s variable to qubits chains, the penalties for equality constraints should be (1) large enough so low-energy configurations do not violate these constraints and (2) the smallest weight that enforces the constraints while enabling precise problem statement (on \(\vc{h}\) and \(\vc{J}\)) and efficient exploration of the search space. An effective procedure incrementally updates weights until the equality constraints are satisfied.
See also the Imprecision of Biases section.
Example#
This example embeds a BQM representing a 30-node signed-social network problem and then looks at the effects of different chain-strength settings.
>>> import networkx as nx
>>> import random
>>> import numpy as np
>>> import dwave_networkx as dnx
>>> import dimod
>>> from dwave.system import DWaveSampler, LazyFixedEmbeddingComposite
>>> import dwave.inspector
...
>>> # Create a problem
>>> G = nx.generators.complete_graph(30)
>>> G.add_edges_from([(u, v, {'sign': 2*random.randint(0, 1) - 1}) for u, v in G.edges])
>>> h, J = dnx.algorithms.social.structural_imbalance_ising(G)
>>> bqm = dimod.BQM.from_ising(h, J)
>>> # Sample on a D-Wave system
>>> num_samples = 1000
>>> sampler = LazyFixedEmbeddingComposite(DWaveSampler())
>>> sampleset = sampler.sample(bqm, num_reads=num_samples)
You can now analyze the solution looking for the affects of your chain-strength setting in various ways.
As a first iteration, it’s convenient to use the Ocean software’s default chain
strength. The LazyFixedEmbeddingComposite
class sets a default chain strength using the
uniform_torque_compensation() function
to calculate a reasonable value. For this problem, with the embedding found
heuristically, it calculated a chain strength of about 7.
>>> print(sampleset.info["embedding_context"]["chain_strength"])
7.614623037288188
You can check the length of the longest chain.
>>> chains = sampleset.info["embedding_context"]["embedding"].values()
>>> print(max(len(chain) for chain in chains))
6
You can verify that the default chain strength for this problem is strong enough so few chains are broken.
>>> print("Percentage of samples with >10% breaks is {} and >0 is {}.".format(
... np.count_nonzero(sampleset.record.chain_break_fraction > 0.10)/num_samples*100,
... np.count_nonzero(sampleset.record.chain_break_fraction > 0.0)/num_samples*100))
Percentage of samples with >10% breaks is 0.0 and >0 is 17.5.
You can also look at the embedding and histograms of solution energies using the Ocean software’s problem inspector tool.
>>> dwave.inspector.show(sampleset)
Figure 58 shows the BQM embedded in an Advantage QPU.
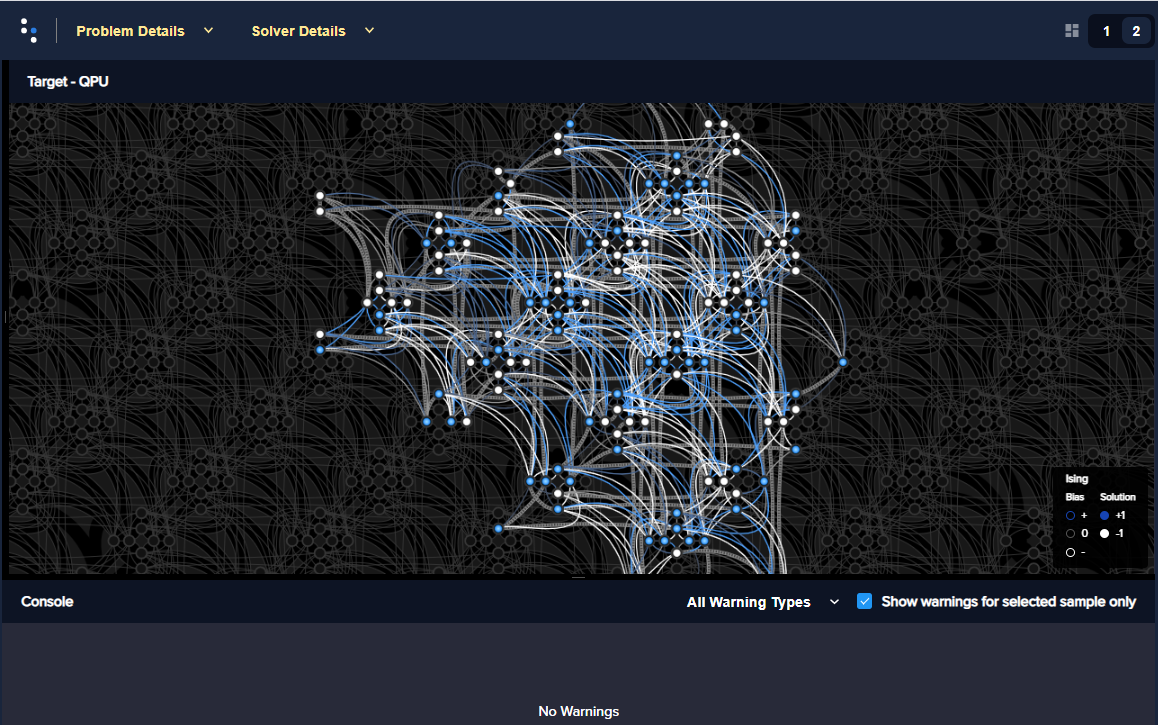
Fig. 58 BQM representing a social-network problem of 30 nodes embedded in an Advantage QPU.#
The following graphs show histograms of the returned solutions’ energies for different chains strengths:
Figure 59 has the default chain strength, which for this problem was calculated as about 7.
Figure 60 has a chain strength manually set to 1 (identical to the maximum bias for the problem). [1]
Figure 61 has a chain strength manually set to 14 (double the default value for this problem).
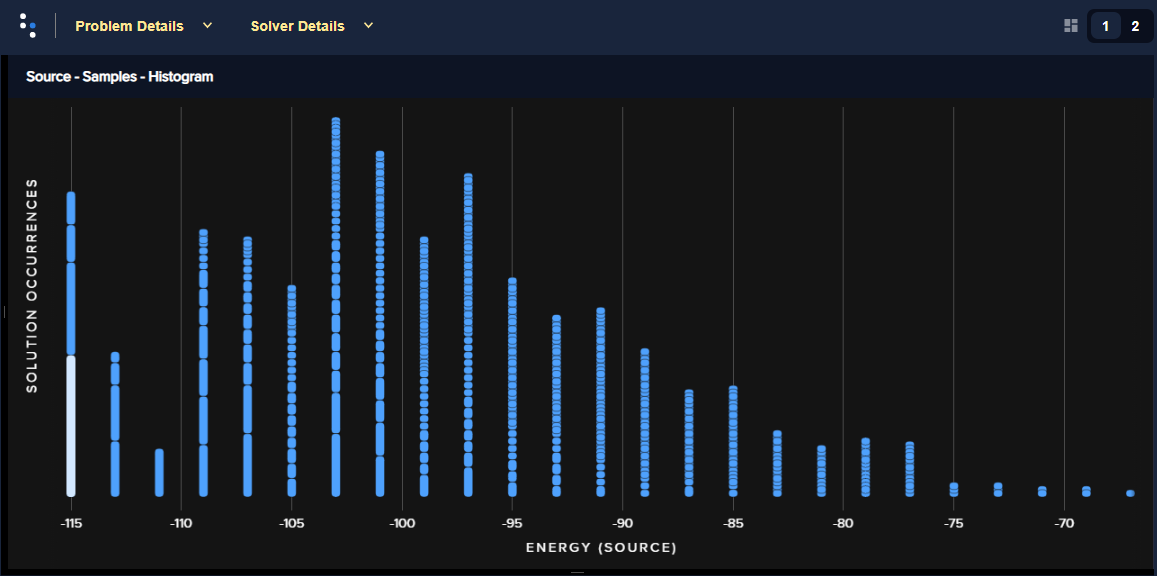
Fig. 59 Energy histogram for the social-network problem with a chain strength of ~7.#
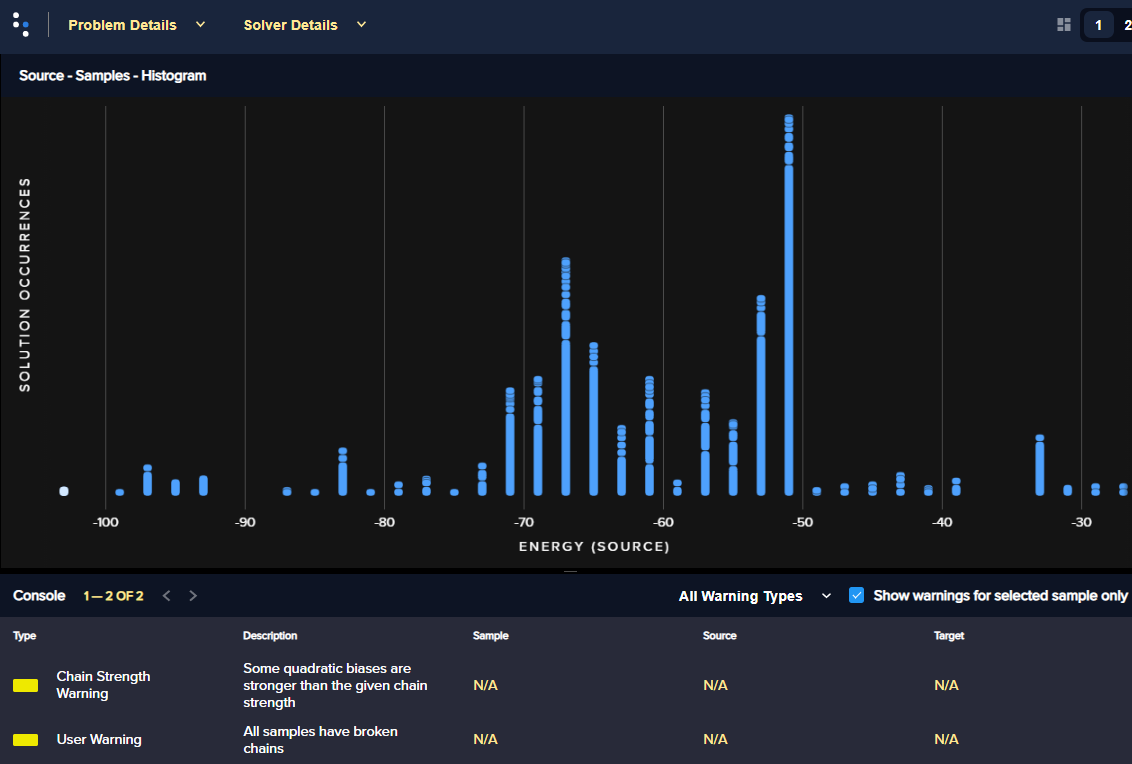
Fig. 60 Energy histogram for the social-network problem with a chain strength of 1.#
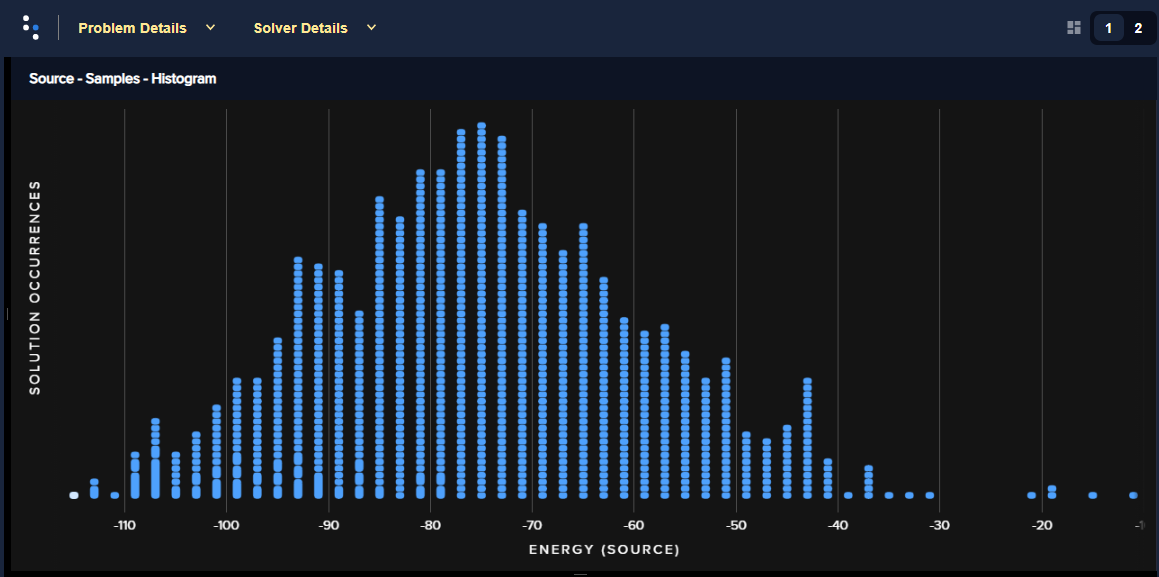
Fig. 61 Energy histogram for the social-network problem with a chain strength of 14.#
You can see that setting the chain strength too low compared to the problem’s biases results in high chain breakage and consequently few good solutions; setting it too high distorts the problem.
Further Information#
The Multiple-Gate Circuit example in the Ocean software documentation is a good introductory example of the effects of setting chain strengths.
The Using the Problem Inspector example demonstrates using the Ocean software’s problem inspector tool for examining embeddings and setting chain strengths.
[Rie2014] studies embedding and parameter setting, and their effects on problem solving in the context of optimization problems.
[Ven2015b] discusses effects of embedding the Sherrington-Kirkpatrick problem.
Embedding Complete Graphs#
Embeddings for cliques (fully-connected graphs) can be very useful: a minor-embedding for a \(K_n\) clique can be used for all minors of that graph. This means that if your application needs to submit to the QPU a series of problems of up to \(n\) variables, having an embedding for the \(K_n\) graph lets you simply reuse it for all those submissions, saving the embedding-computation time in your application’s runtime execution.
Using a clique embedding can have a high cost for sparse graphs because chain lengths increase significantly for high numbers of variables.
Example: Largest Cliques on the Chimera Topology#
The largest complete graph \(K_V\) that is a minor of a \(M\times N\times L\) Chimera graph has \(V=1+L\min(M,N)\) vertices. For example, 65 vertices is the theoretical maximum on a C16 Chimera graph (a \(16 {\rm x} 16\) matrix of 8-qubit unit cells for up to[2] \(2MNL=2 \times 16 \times 16 \times 4=2048\) qubits), which was the topology of the D‑Wave 2000Q system.
The yield of a working graph is typically less than 100%.
Example: Chain Lengths for Cliques on Pegasus and Chimera Topologies#
Table 31 shows some example embeddings of complete graphs versus chain lengths for both QPU topologies with 95% yields. For a given maximum chain length, you can embed cliques of about the following sizes in Pegasus P16 and Chimera C16 topologies with working graphs simulating 95% yield (by random removal of 5% of nodes and 0.5% of edges to represent inactivated qubits and couplers):
Chain Length |
Chimera Topology |
Pegasus Topology |
|---|---|---|
1 |
\(K_2\) |
\(K_4\) |
2 |
\(K_4\) |
\(K_{10}\) |
4 |
\(K_{12}\) |
\(K_{30}\) |
10 |
\(K_{28}\) |
\(K_{71}\) |
For a Pegasus graph with 100% yield the largest complete graph that is embeddable is \(K_{150}\) with chain length of 14. QPUs typically do not achieve 100% yield.
Example: Clique-Embedding a Sparse BQM#
Figure 62 shows an example BQM constructed from
a sparse NetworkX graph,
chvatal_graph(). This example embeds the BQM
onto an Advantage QPU in two ways: (1) using the standard
minorminer heuristic of
the EmbeddingComposite class and (2) using
a clique embedding found by the
DWaveCliqueSampler class.
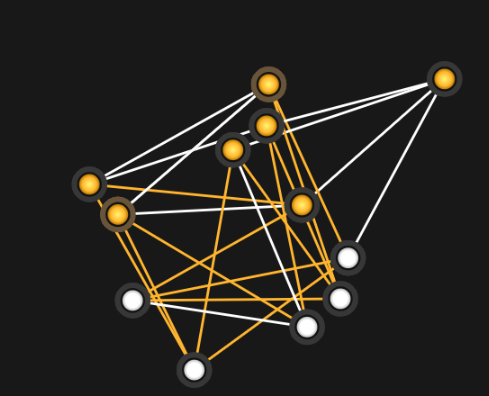
Fig. 62 BQM based on a sparse graph.#
>>> from dwave.system import DWaveSampler, EmbeddingComposite, DWaveCliqueSampler
>>> import networkx as nx
>>> import dimod
>>> import random
>>> import dwave.inspector
...
>>> # Create a small, sparse BQM from a NetworkX graph
>>> G = nx.generators.small.chvatal_graph()
>>> for edge in G.edges:
... G.edges[edge]['quadratic'] = random.choice([1,-1])
>>> bqm = dimod.from_networkx_graph(G,
... vartype='BINARY',
... edge_attribute_name='quadratic')
>>> sampleset = EmbeddingComposite(DWaveSampler()).sample(bqm, num_reads=1000)
>>> sampleset_clique = DWaveCliqueSampler().sample(bqm,
... num_reads=1000)
The following graphs show both embeddings:
Figure 63 is an embedding found for the sparse graph.
Figure 64 is a clique embedding in which the BQM graph is a minor.
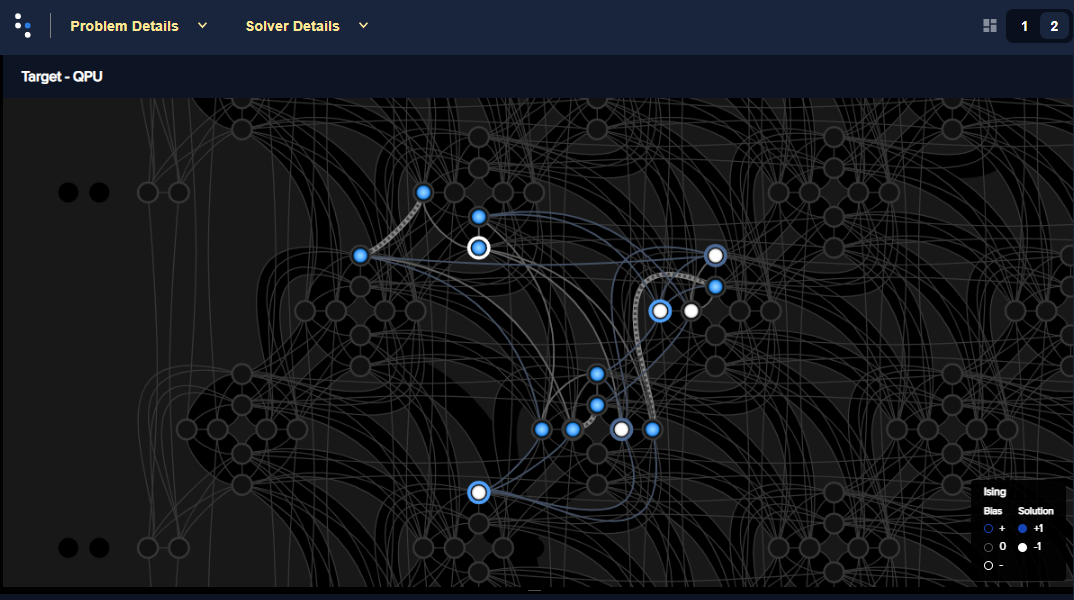
Fig. 63 Embedding found for the sparse graph of the problem.#
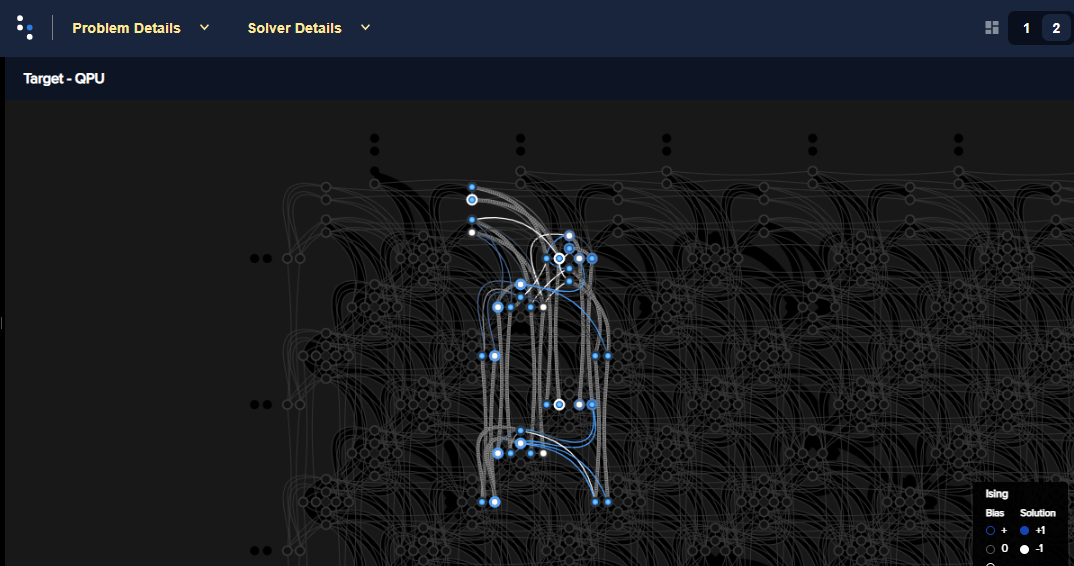
Fig. 64 Clique embedding that includes the sparse graph of the problem.#
Clearly the clique embedding requires more and longer chains.
Further Information#
[Pel2021] proposes a method of parallel quantum annealing that makes use of available qubits by embedding several small problems in the same annealing cycle.
[Zbi2020] proposes two algorithms, Spring-Based MinorMiner (SPMM) and Clique-Based MinorMiner (CLMM), for minor-embedding QUBO problems into Chimera and Pegasus graphs.
Exploring the Pegasus Topology Jupyter Notebook.
Reusing Embeddings#
For problems that vary only the biases and weights on a fixed graph, you can set a good embedding once before submitting the problem to the QPU. There is no need to recompute the embedding (a time-consuming operation) for every submission.
Pre-embedding Local Constraint Structures#
The structure of some problems contains repeated elements; for example, the multiple AND gates, half adders, and full adders in the Factoring example. Such problems may benefit from being embedded with repeating block structures for the common elements, with connectivity then added as needed.
Example#
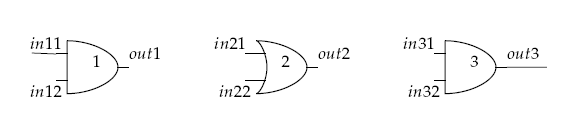
Fig. 65 Circuit of three Boolean gates.#
This small example pre-embeds three Boolean gates.
You can embed a BQM representing an AND or OR gate in a repeating structure of the Pegasus topology, a \(K_{4,4}\) biclique with additional couplers connecting some horizontal and vertical qubits.
>>> import minorminer
>>> import dwave_networkx as dnx
>>> from dimod.generators import and_gate, or_gate
...
>>> pegasus_k44 = dnx.pegasus_graph(2, node_list=[4, 5, 6, 7, 40, 41, 42, 43])
...
>>> bqm_and1 = and_gate('in11', 'in12', 'out1')
>>> embedding_and = minorminer.find_embedding(list(bqm_and1.quadratic.keys()), pegasus_k44)
>>> embedding_and
{'in12': [40], 'in11': [4], 'out1': [41]}
...
>>> bqm_or2 = or_gate('in21', 'in22', 'out2')
>>> embedding_or = minorminer.find_embedding(list(bqm_or2.quadratic.keys()), pegasus_k44)
>>> embedding_or
{'in22': [4], 'in21': [41], 'out2': [40]}
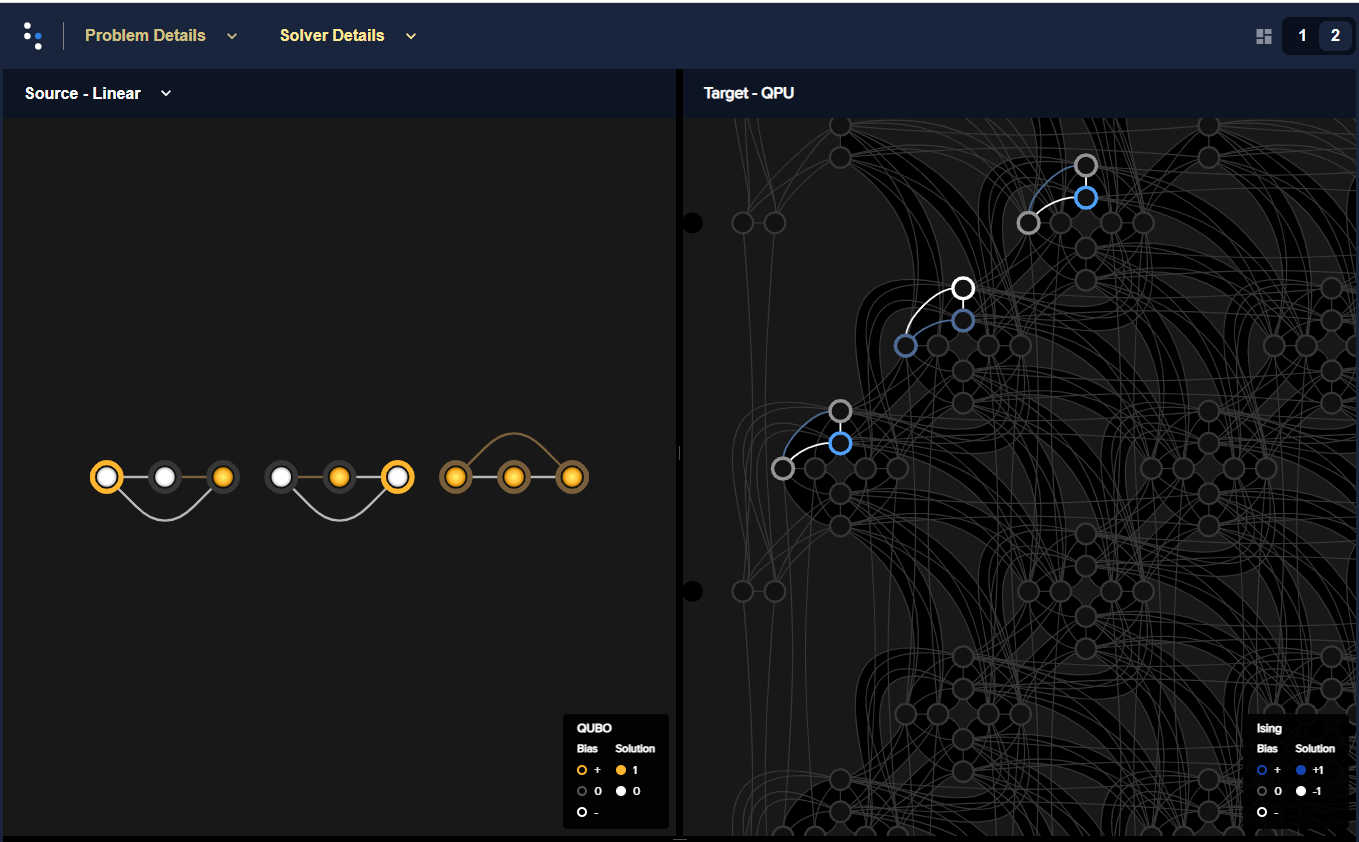
Fig. 66 Circuit of three Boolean gates pre-embedded in an Advantage QPU.#
Further Information#
[Ada2015] describes embedding an RBM on the D‑Wave system by mapping the visible nodes to chains of vertical qubits and hidden nodes to chains of horizontal qubits.
Virtual Graphs#
Important
The virtual graph feature is deprecated due to improved calibration of
newer QPUs: Ocean software’s
VirtualGraphComposite class will be
removed in a future release. To calibrate chains for residual biases, follow
the instructions in [Che2023].
The D‑Wave virtual graph feature simplifies the process of
minor-embedding by enabling you to more easily create, optimize, use, and reuse
an embedding for a given working graph. When you submit an embedding and specify
a chain strength using the
VirtualGraphComposite class, it automatically
calibrates the qubits in a chain to compensate for the effects of unintended
biases—see
integrated control errors (ICE) 1—
caused by QPU imperfections.
Further Information#
[Dwave6] is a white paper describing measured performance improvements from using virtual graphs.